Convexity and Quantum Physics







Remember: \({\color{green}\langle \Psi|\color{blue}|\Psi\rangle}\ge 0\)
Of course \({\color{green}\langle 0 | x \color{blue}x | 0 \rangle} \ge 0\) and \({\color{green}\langle 0 | p \color{blue}p | 0 \rangle} \ge 0\). So: \(\langle \hat H \rangle \ge 0\).
We can do better, by using the uncertainty principle: \([x,p] = i\hbar\).
Take \(|\Psi\rangle = (\hat x+i\hat p)|0\rangle\). \[ \langle (\hat x-i\hat p) (\hat x+i\hat p) \rangle = \langle \hat x^2 \rangle +i\langle[\hat x,\hat p]\rangle +\langle \hat p^2 \rangle \ge 0 \]
This is the classic proof that \(\langle \hat H \rangle \ge \frac \hbar 2\) for the harmonic oscillator.
Define \(|\Psi\rangle = (1 + \sigma_x)|0\rangle\) \[ \langle \Psi | \Psi\rangle \ge 0 \Longrightarrow \langle 2 + 2\sigma_x \rangle \ge 0 \Longrightarrow \langle \sigma_x \rangle \ge -1 \]
So \(\langle H\rangle \ge -\mu\) (as expected!)
Both bounds happen to be tight. This won't always happen.
Let's move from states to operators!
\[\color{green} \langle \mathcal O^\dagger \mathcal O \rangle \ge 0 \]Consider a basis of operators \(\mathcal O_1,\ldots\mathcal O_N\). We can build a matrix \[ M = \left(\begin{matrix} \langle \mathcal O_1^\dagger \mathcal O_1 \rangle & \langle \mathcal O_1^\dagger \mathcal O_2\rangle & \cdots \\ \langle \mathcal O_2^\dagger \mathcal O_1 \rangle & \langle \mathcal O_2^\dagger \mathcal O_2\rangle & \cdots \\ \vdots & \vdots & \ddots \end{matrix}\right) \]
The matrix \(M\) is positive semi-definite!
Proof: for any vector \(v\), consider the operator \(\mathcal O = \sum_i v_i \mathcal O_i\). \[ v^\dagger M v = \langle (\vec v \cdot \mathcal {\vec O})^\dagger (\vec v \cdot \mathcal {\vec O}) \rangle = \langle \mathcal O^\dagger \mathcal O \rangle \ge 0 \]
With a complete set of operators, this sums up the entire positivity axiom.
Let \(C\) be an \(N \times N\) matrix. We wish to find a positive semi-definite matrix \(X\) \[ \text{minimizing }\;\mathrm{Tr}\;CX \] subject to linear constraints on the matrix elements of \(X\).
In our context, \(C\) specifies the Hamiltonian, and the linear constraints follow from the commutation relations.
Example: \(\langle xp\rangle - \langle px\rangle = i\hbar\)
Here's a basis of operators: \(\{1, \sigma_x, \sigma_y, \sigma_z\}\). (In fact this basis is complete.)
\[\color{green} \left(\begin{matrix} 1 & \langle \sigma_x \rangle & \langle \sigma_y \rangle & \langle \sigma_z \rangle\\ \langle \sigma_x \rangle & 1 & i \langle \sigma_z \rangle & -i \langle \sigma_y \rangle\\ \langle \sigma_y \rangle & -i \langle \sigma_z \rangle & 1 & i\langle \sigma_x \rangle\\ \langle \sigma_z \rangle & i\langle \sigma_y \rangle & -i \langle \sigma_x \rangle & 1 \end{matrix}\right)\succeq 0 \]Note that any assignment of expectation values obeying the above constraint corresponds to some density matrix \(\rho\).
For \(H = -\mu \sigma_x\), only the upper-left \(2\times 2\) minor is needed. \[ \left|\begin{matrix} 1 & \langle \sigma_x \rangle\\ \langle \sigma_x \rangle & 1 \end{matrix}\right|\ge 0 \Longrightarrow 1 - \langle \sigma_x \rangle^2 \ge 0 \]
We can't use a complete basis. Let's start with \(\{1,x,p\}\). \[\color{green} \left(\begin{matrix} 1 & \langle x\rangle & \langle p \rangle\\ \langle x \rangle & \langle x^2 \rangle & \langle xp \rangle\\ \langle p \rangle & \langle xp \rangle + i\hbar & \langle p^2 \rangle \end{matrix}\right)\succeq 0 \]
This is just one small part of the "full" SDP, but it represents several important constraints!
Using the lower \(2\times 2\) minor: \[ \left|\begin{matrix} \langle x^2 \rangle & \langle xp \rangle\\ \langle xp \rangle + i\hbar & \langle p^2 \rangle \end{matrix}\right| = \langle x^2 \rangle \langle p^2\rangle - \langle xp\rangle^2 - i \hbar \langle xp \rangle \ge 0 \Longrightarrow \langle x^2\rangle \langle p^2\rangle \ge \hbar \]
Adding more operators can only make the bound stricter.
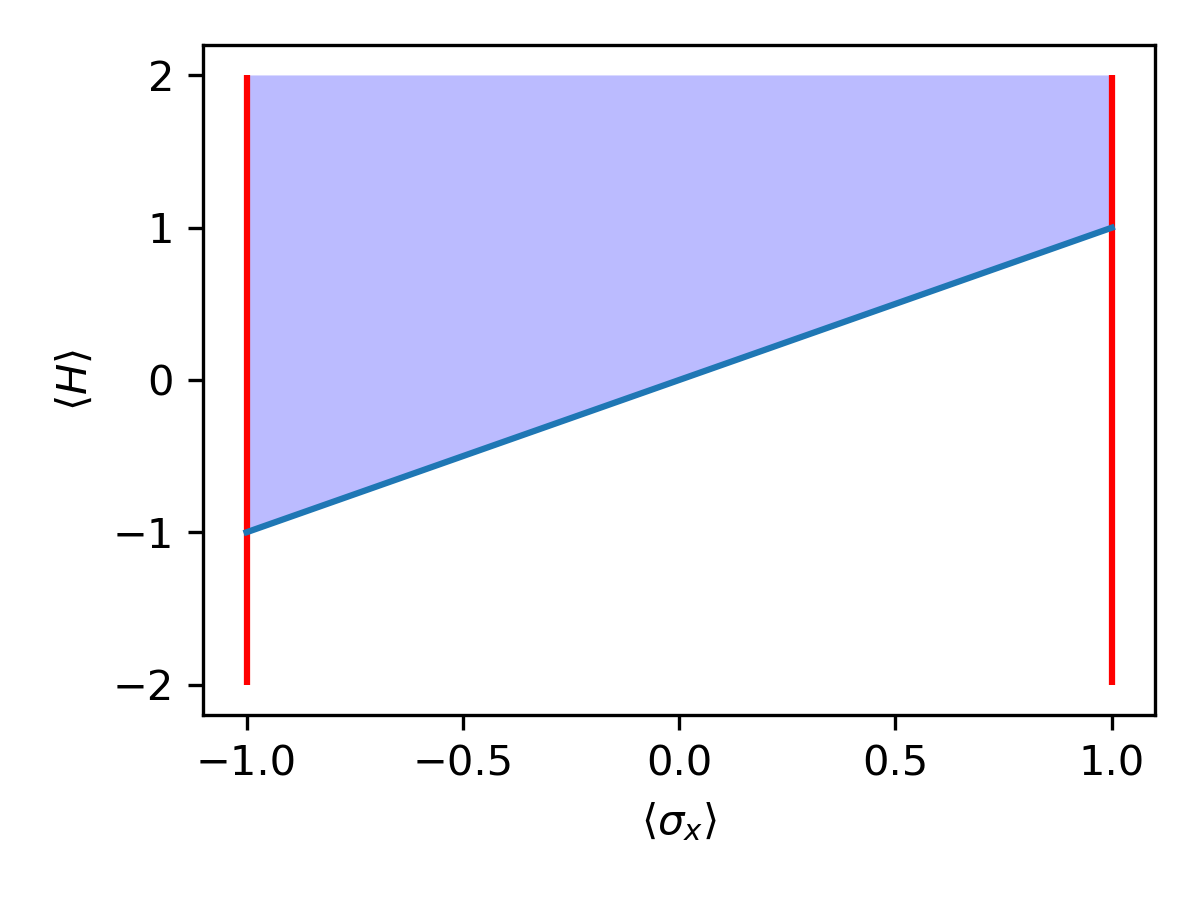
From which we see that \(\color{blue}\langle H \rangle \ge -1\)
Similarly, \(\color{blue}\langle H \rangle \ge \frac 1 2\)
In general, if we can write \[ H = C + \mathcal O_1^\dagger \mathcal O_1 + \mathcal O_2^\dagger \mathcal O_2 + \cdots \]
then the bound \(\color{blue}\langle H \rangle \ge C\) follows immediately.
Quantum information
Conformal bootstrap: a history lesson
Computational applications (matrix models, lattice field theories)
Setup: Alice samples a random number \(i \in 1\ldots N\), with probability \(p_i\). Alice sends a quantum state \(\rho_i\) to Bob. Bob must make a measurement and guess \(i\).
How well can Bob do?
Bob will measure onto some set of projectors \(\{E_j\}\), and reply \(j\) with probability \[ P_j(|\psi\rangle) = \mathrm{Tr}\; E_j \rho_i \] We want to maximize the success probability, that is \[ \sum_i p_i \mathrm{Tr}\; \rho_i E_i \] subject to \[ E_i \succeq 0 \text{ and } \sum_i E_i = 1 \]
Surprise! It's an SDP!
Alice and Bob each have access to one half of a quantum system. Alice can measure operators \(E_\alpha\), and Bob \(E_\beta\). A quantum correlation is: \[ P_{\alpha\beta} = \mathrm{Tr}\;E_\alpha E_\beta \rho \]
Which probabilities \(P_{\alpha\beta}\) are achievable quantum correlations?
Answer: \(\Gamma_{ij} = \mathrm{Tr}\; S_i^\dagger S_j \rho \succeq 0\). So, we require that such a \(\Gamma\) exists, compatible with the given probabilities (a linear condition). \[\color{green} \mathcal S_1 = \{E_\alpha\} \cup \{E_\beta\} \;\text{ ; }\; \mathcal S_2 = \{E_\mu E_\nu\} \;\text{ ; }\; \cdots \]
Tsirelson's problem: can every quantum correlation be approximated by a system of finite Hilbert space dimension?
No (!)

Finding a global minimum is hard, in general.
For convex functions, it's much easier
Current tools for solving SDPs: SDP-A, MOSEK, SDPB
There is certainly room for improvement in this space.
The original dream: construct an S-matrix purely from symmetries and consistency conditions.
Circumvents the need for a sensible definition of field theory.
Fell out of favor as QCD became understood.

\(\sim 40\) years pass...
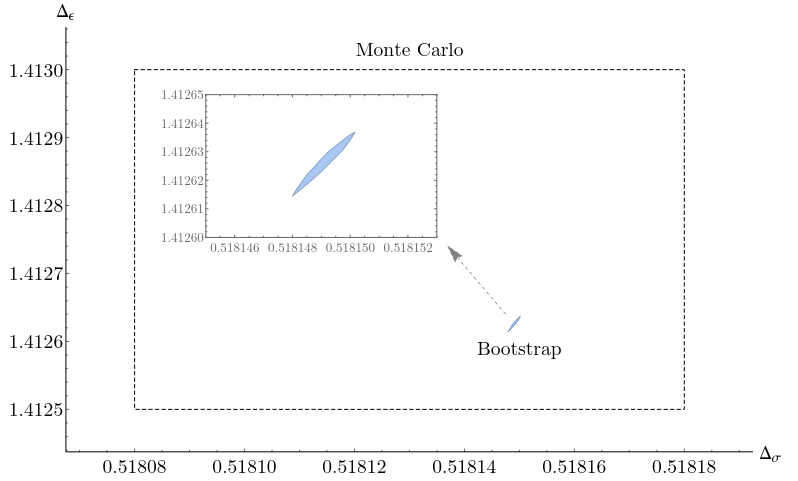
Conformal bootstrap: modern numerical techniques allow the bootstrap program to strongly constrain the space of conformal field theories, purely from symmetries and consistency.
Now "bootstrap" and "semi-definite programming" are somewhat synonymous.
A conformal field theory is:
Why do we care?
At asymptotically high or low energies, any field theory approaches a conformal fixed point.
Also, lamppost effect: we study these because they're (relatively) easy.
To study individual eigenstates, we can impose: \[ \langle H \mathcal O \rangle = E \langle \mathcal O \rangle \]
For the anharmonic oscillator, this yields constraints like:

The allowed region is not convex!
Let \(X,P\) be \(N\times N\) Hermitian matrices of operators, obeying \[ [P_{ij},X_{kl}] = -i \delta_{ik} \delta{jl} \]
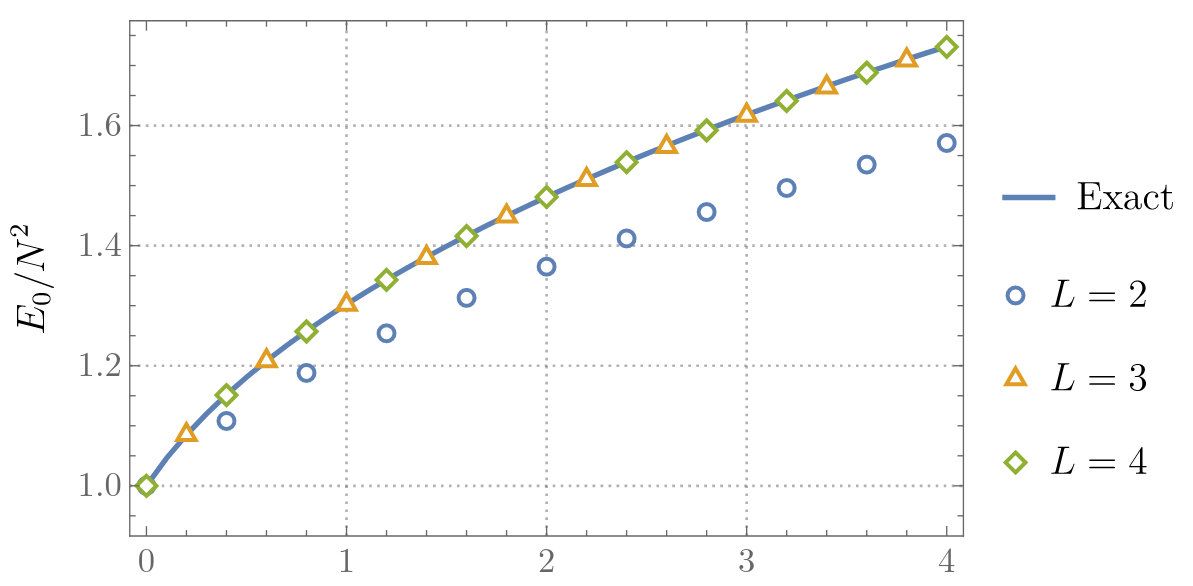
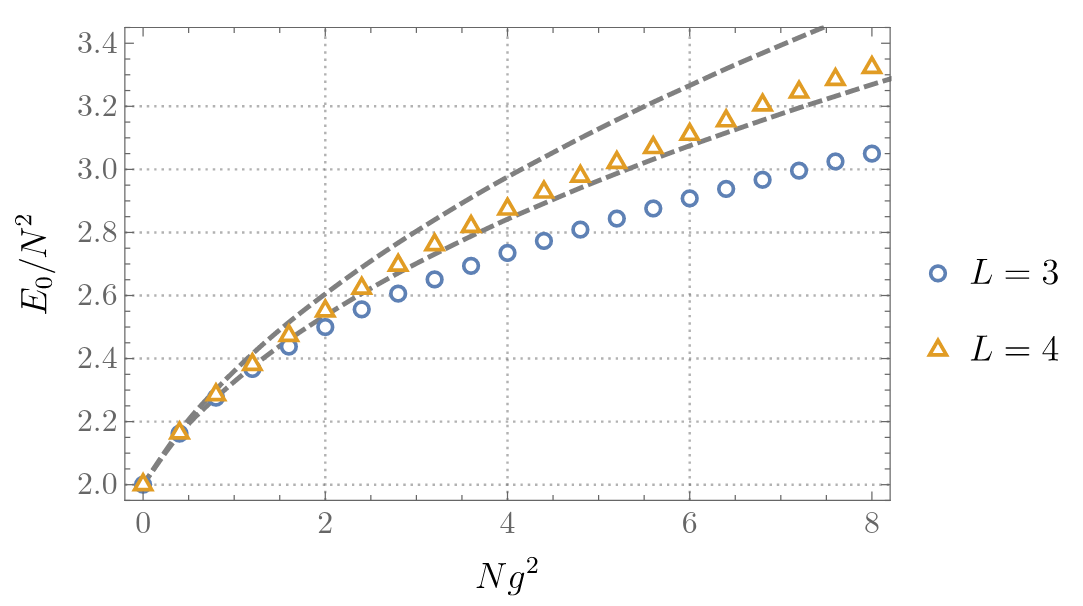
Some Hamiltonians \[ \color{green} H_{\mathrm{easy}} = \mathrm{Tr}\; P^2 + \mathrm{Tr}\;X^2 + \frac{g}{N}\mathrm{Tr}\;X^4 \] \[\color{red} H_{\mathrm{harder}} = \mathrm{Tr}\; P_X^2 + \mathrm{Tr}\; P_Y^2 + m^2 \mathrm{Tr}\;(X^2 + Y^2) - \mathrm{Tr}\;g^2[X,Y]^2 \]
Matrix models are quantum mechanical and consistent.
Conjecture: Larger matrix models (e.g. BFSS) exhibit emergent spacetime.
Each lattice site has a degree of freedom with Hilbert space \(\mathcal H_1\). The whole system has Hilbert space $$ \mathcal H = \mathcal H_1 \otimes \mathcal H_1 \otimes \cdots $$
Some Hamiltonian \(H\) couples the different lattice sites. For a spin system, we might have $$ H = \sum_{\langle i j\rangle} \sigma_z(i) \sigma_z(j) + \sum_i \sigma_x(i) $$
When correlations are large, the lattice structure is irrelevant, hence "field theory".
With \(m = 0.2\)
Operators:
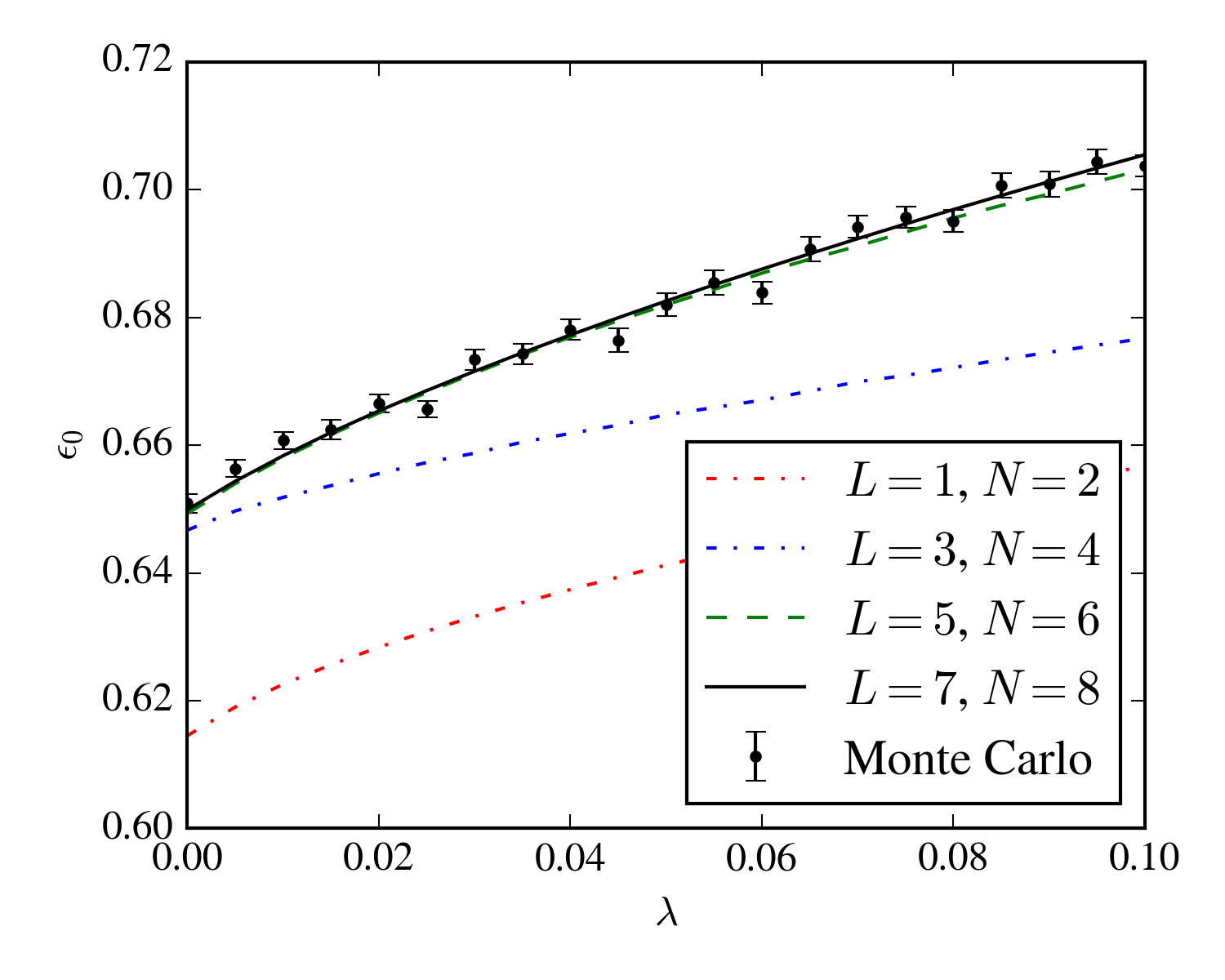
Monte Carlo (i.e. lattice QCD) methods are powerful, but fail for relativistic theories at finite fermion (proton - antiproton) density.
First noted in 1990. Not well-understood in general.
Makes it difficult to study:

The lattice Thirring model (staggered fermions):
At finite chemical potential, lattice Monte Carlo exhibits the sign problem.
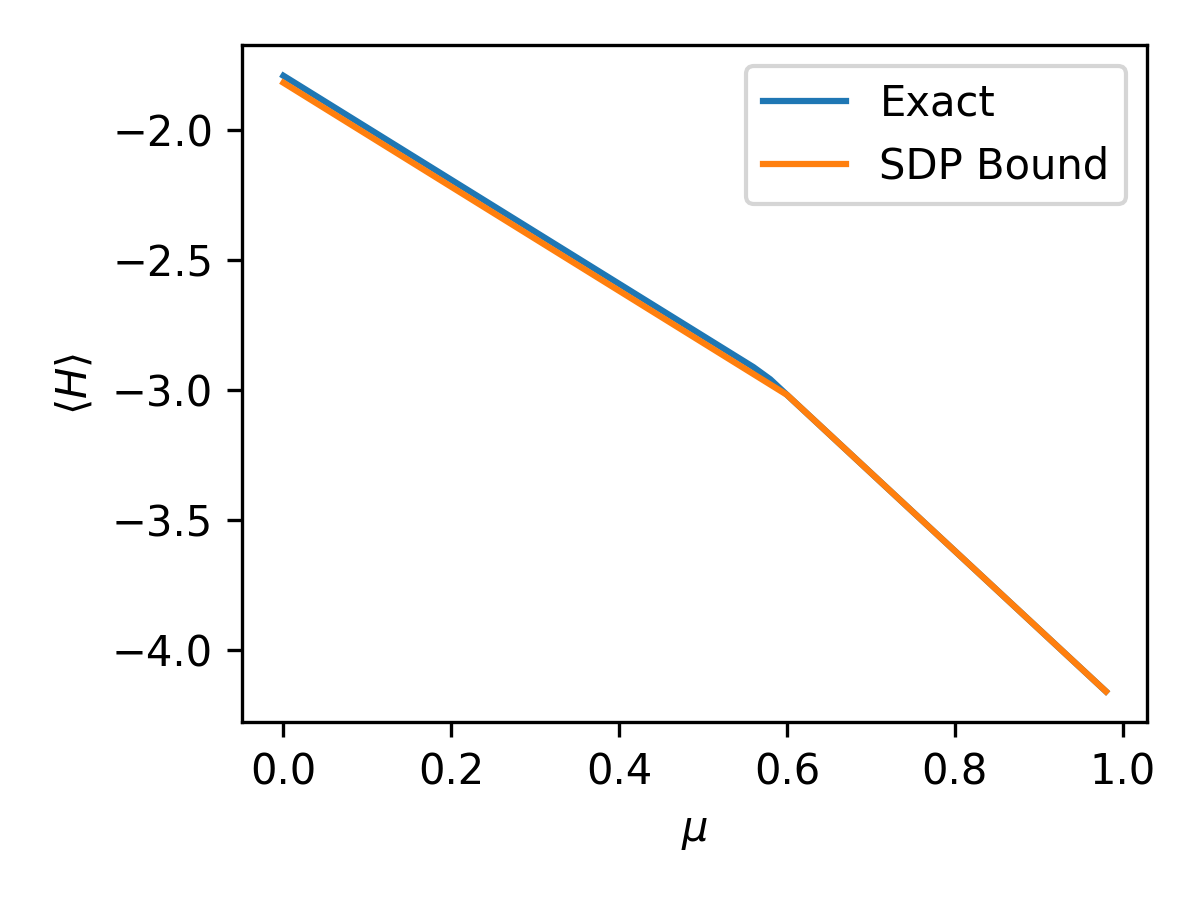
No evidence of a sign problem