QCD is a non-perturbative theory. (There's no small parameter about which to Taylor expand.)
At every link lives a unitary matrix. $$ U_{yx} \in SU(3) $$
The action is a sum over all `plaquettes'. $$ S = \sum_P \mathrm{Re\,Tr\,} P $$
This is a theory of with a finite number of degrees of freedom. Expectation values are given by: $$ \left<\mathcal O\right> = \frac{\int \mathcal D U\;e^{-S[U]} \mathcal O[U]}{\int \mathcal D U\;e^{-S[U]}}$$
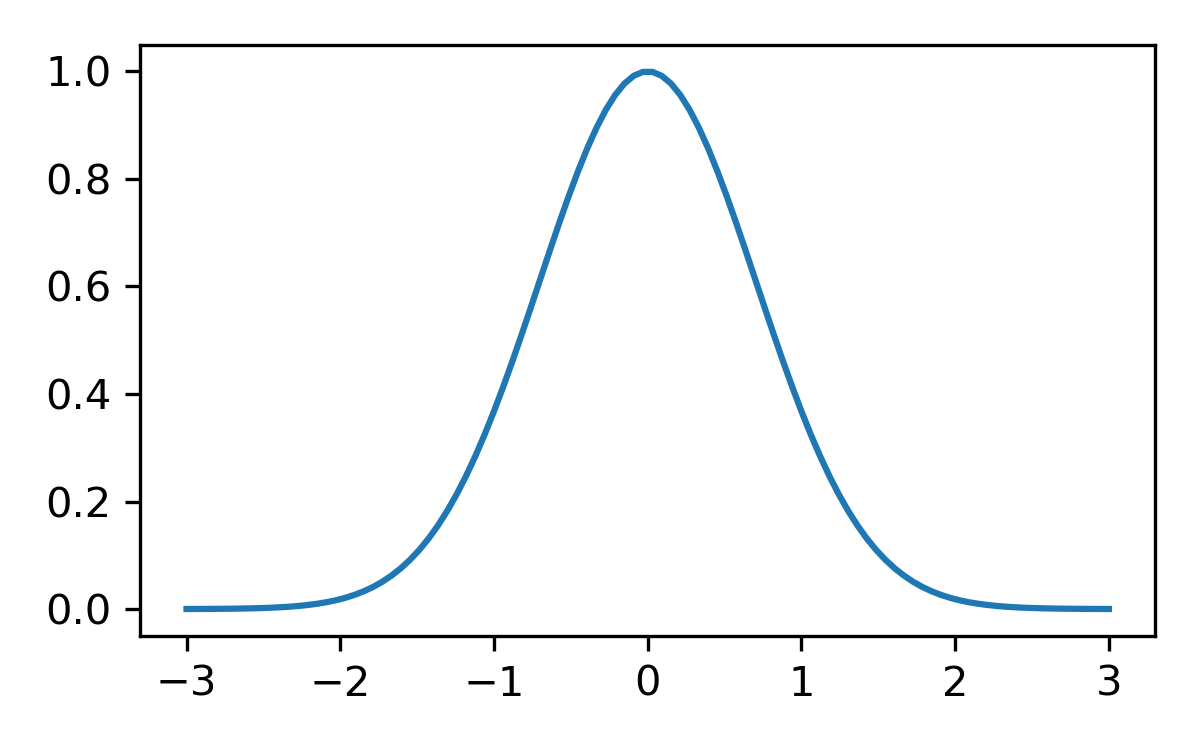$$ \int f \approx 1 \pm 0.5$$
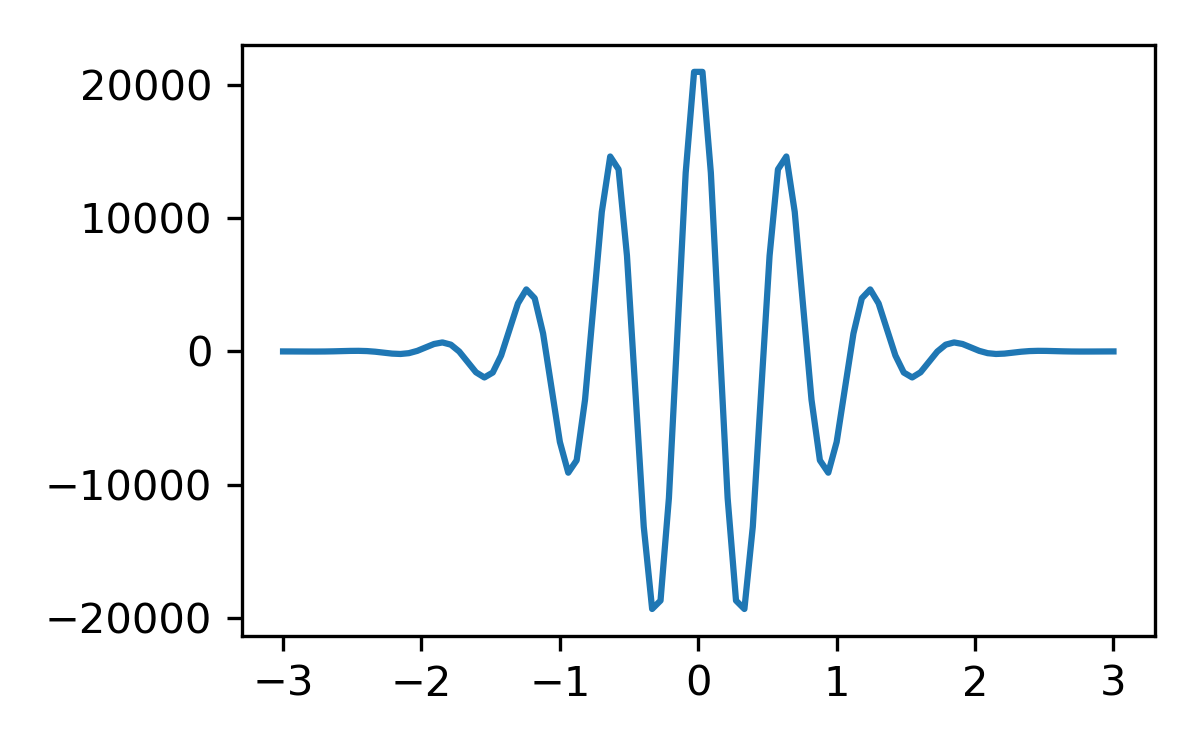$$ \int f \approx 0 \pm 10^4 $$
Calculations that have sign problems:
Closely related, but mild: determining the mass of a proton
Calculations without sign problems:
Set up an analogy between the quantum computer and the system to be simulated, and treat the computer like a (perfectly controlled) laboratory.
This is a spin from QM.
What's the Hilbert space? $$ \mathcal H = \mathcal H_1 \otimes \cdots \otimes \mathcal H_1 \;\text{ where } \mathcal H_1 = \mathrm{span}\{|0\rangle,|1\rangle\} $$
In other words, superpositions of all possible bitstrings. $$ \mathcal H = \mathrm{span}\{|00\cdots\rangle,|10\cdots\rangle,|01\cdots\rangle,\cdots\} $$
All operations must be unitary (conservation of probability). On one qubit:
On two qubits, the controlled-not operation:
These fundamental gates are sufficient to construct any unitary we want.
In principle, we measure any Hermitian operator. In practice, we measure \(\sigma_z\) acting on each qubit. $$\Psi = \alpha|0\rangle + \beta|1\rangle$$
Each measurement yields \(1\) or \(0\). Probability of \(1\) is \(\langle\Psi|1\rangle\langle 1|\Psi\rangle = |\beta|^2\).
Thus, we require many measurements for a precise result. This is "shot noise".
Hermitian operators are exactly those which may appear as terms in the Hamiltonian.
Current best: \(\sim 50\) qubits.
Each qubit can undergo \(\lesssim 10\) operations before decohering.
Are large processors worth it?
This restricts the set of possible operations, as well. We only have permutations:
Example: two-bit adder $$ \begin{align} |00\rangle |00\rangle &\rightarrow |00\rangle |00\rangle \\ |01\rangle |00\rangle &\rightarrow |01\rangle |01\rangle \\ |10\rangle |00\rangle &\rightarrow |10\rangle |01\rangle \\ |11\rangle |00\rangle &\rightarrow |11\rangle |10\rangle \\ \end{align} $$
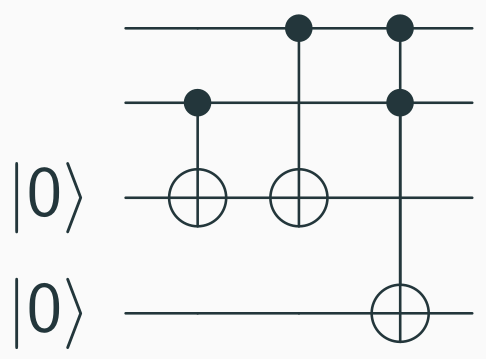
In general, given a classical circuit for \(f(x)\), we can obtain $$ |x\rangle|0\rangle \rightarrow |x\rangle |f(x)\rangle $$
Assume we can evolve under \(A\) and \(B\). How to get evolution under \(H\)? $$ e^{-i H \epsilon} \approx {\color{blue}e^{-i A \epsilon}} {\color{green}e^{-i B \epsilon}} $$
So, time-evolve by rapidly alternating between two Hamiltonians $$ e^{-i H t} \approx \left({\color{blue}e^{-i A \epsilon}} {\color{green}e^{-i B \epsilon}}\right)^{t / \epsilon} $$
Each lattice site has a degree of freedom with Hilbert space \(\mathcal H_1\). The whole system has Hilbert space $$ \mathcal H = \mathcal H_1 \otimes \mathcal H_1 \otimes \cdots $$
Some Hamiltonian \(H\) couples the different lattice sites. For a spin system, we might have $$ H = \sum_{\langle i j\rangle} \sigma_z(i) \sigma_z(j) + \sum_i \sigma_x(i) $$
When correlations are large, the lattice structure is irrelevant, hence "field theory".
The Hamiltonian of a free particle moving on \(G = SU(3)\): $$ H = -\nabla_\ell^2 $$
Hilbert space is \(\mathbb C G\), the space of complex functions on \(G\).
We can work with momentum eigenstates instead.
The Hamiltonian is gauge-invariant. $$ H = -\beta_K\sum_\ell \nabla_\ell^2 + \beta_P\sum_P \mathrm{Re\,Tr\,}P $$
$$
\mathcal H = \mathbb C G \otimes \mathbb C G \otimes \cdots
$$
Here's a projection operator: $$ P |U_{12}\cdots\rangle = \int(\mathrm{d}V_1 \mathrm{d}V_2\cdots)|(V^\dagger_2 U_{12} V_1)\cdots\rangle $$
Four states, naively: \(|00\rangle\), \(|01\rangle\), \(|10\rangle\), \(|11\rangle\). But these are not gauge-invariant!
Gauge transformation takes \(00 \leftrightarrow 11\) and \(01 \leftrightarrow 10\). $$ \color{green} |00\rangle + |11\rangle \;\text{ and }\; |01\rangle + |10\rangle $$
We need a mapping between the Hilbert spaces. Locality is nice. $$ \mathcal H_1 \leftrightarrow \mathcal H_1^{\mathrm{QC}} $$
This induces a "nice" map \(\mathcal H \leftrightarrow \mathcal H^{\mathrm{QC}}\)
Implement \(e^{-i H t}\) via Suzuki-Trotter
One link only
Diagonal in Fourier space
Mutually commuting terms
Four links
Diagonal (in our basis)
Mutually commuting terms
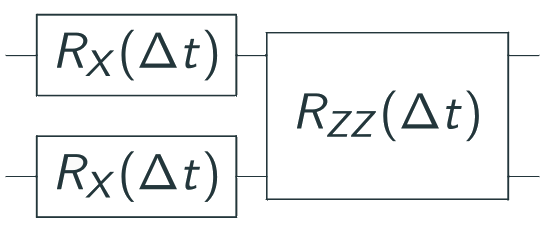
We'd like to simulate \(SU(3)\), but \(\mathbb C SU(3)\) is infinite-dimensional.
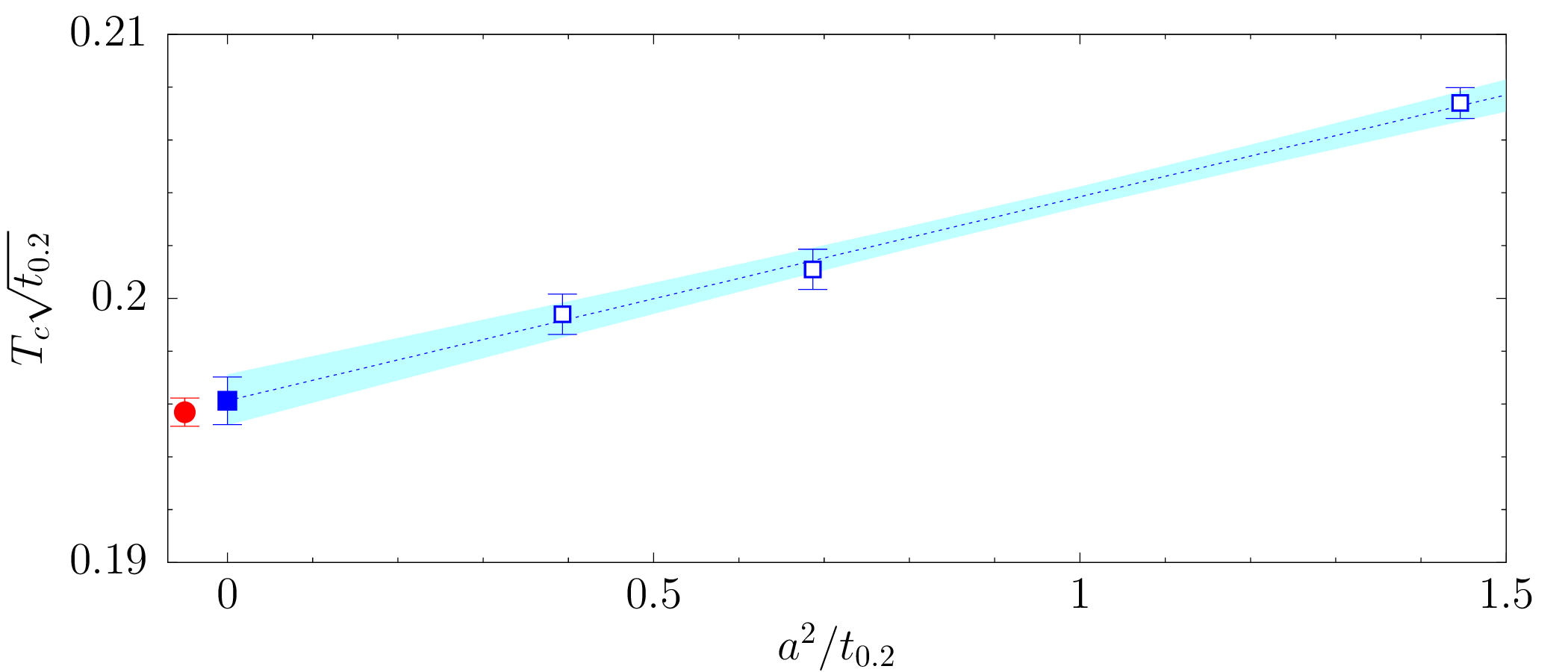
After adding an extra term to the action... $$ S=-\sum_p \left(\frac{\beta_0}{3}\mathrm{Re\,Tr\,} U_p +\beta_1\mathrm{Re\,Tr\,} U_p^2\right) $$
Construct a dimensionless quantity from: Wilson flow, critical temperature
Particle masses not yet measured...
The physical Hilbert space is not \(\mathbb C S(1080) \otimes \mathbb C S(1080) \otimes\cdots\).
But, the Hilbert space on the quantum computer is isomorphic to that space!
If we start in a gauge-invariant state, we stay gauge-invariant.
The hadronic tensor captures nonperturbative (in QCD coupling) information about the proton. For electron-proton scattering, to leading order in \(\alpha_{\mathrm{QED}}\): \[ \frac{{\mathrm d}^2\sigma}{\mathrm{d} x\;\mathrm{d} y} = \frac{\alpha^2 y}{Q^4} L_{\mu\nu} W^{\mu\nu} \]
Naive state preparation: couple to a heat bath and cool the system. Expensive!
Alternative: adiabatic state preparation
Other proposals:
arXiv:1709.08250)1908.07051)Hard to analyze, impossible to test
Take a time-varying (slowly) Hamiltonian \(H(t)\).
Prepare an eigenstate of \(H(0)\), with a gap of \(\Delta\).
When \(\dot H / \Delta^2 \ll 0\), time-evolution will keep us in the eigenstate.
Time needed to prepare ground state: \(\Delta^{-2}\)
Restrict to a certain sector of Hilbert space:
How do we measure \(e^{i H t}J_0(x)e^{-i H t} J_0(0)\)? \[ H(t) = H_0 + \epsilon \delta(t) J^\nu(\vec 0) \]
Linear response: differentiate with respect to \(\epsilon\) \[ \frac{\partial}{\partial \epsilon} \langle e^{i H t} J^\mu(\vec x) e^{-i H t}\rangle \]
Shear/bulk viscosity, conductivity, etc... $$ \eta = \frac T V \int \mathrm{d}^4 x\; \langle \pi_{ij}(x) \pi_{ij}(0) \rangle $$ $$ \sigma \sim \int \mathrm{d}t\;\langle j(t) j(0)\rangle $$
The expectation value still has the form of linear response: $$ H(t) = H_0 + \epsilon \delta(t) \pi_{xy}(0) $$
State preparation dominates the gate cost of the calculation.
Classical lattice methods are very good at simulating thermodynamics; can't do real-time.
Quantum computers simulate real-time evolution easily; thermodynamics can be expensive.
Boltzmann factor \(p_i \propto e^{-\beta E_i}\)
Partition function \(Z = \sum_i e^{-\beta E_i}\)
Expectation values \(\langle \mathcal O\rangle = \sum_i p_i \mathcal O_i\)
Density matrix \(\rho = e^{-\beta H}\)
Partition function \(Z = \mathrm{Tr\,}\rho\)
Expectation values \(\langle \mathcal O\rangle = Z^{-1} \mathrm{Tr\,} \mathcal O \rho\)
Several ways of turning \(\rho\) into a probability distribution to sample. We could take the diagonal $$ \langle \mathcal O \rangle = \frac{\sum_i \rho_{ii} \mathcal O_{ii}}{\sum_i \rho_{ii}} $$
Equality holds when \(\mathcal O\) is diagonal. (Common in lattice QCD.)
We want \(\langle \mathcal O(t)\rangle\); the operator isn't diagonal! $$ \langle \mathcal O(t)\rangle = \frac{\sum_{ij} \rho_{ij} \mathcal O(t)_{ji}}{\sum_{i}\rho_{ii}} = \left(\frac{\sum_{ij} \rho_{ij} \mathcal O(t)_{ji}}{\sum_{ij} \rho_{ij}}\right)\color{red}\underbrace{\left(\frac{\sum_{ij} \rho_{ij}}{\sum_{i} \rho_{ii}}\right)}_{\mathrm{Normalization}} $$
Therefore: sample pairs of states \(|i\rangle\langle j|\), distributed by \(\rho_{ij}\).
How to compute \(\mathcal O(t)_{ij}\)? This part is done on a quantum computer.
Preparing a basis state \(|i\rangle\) is cheap. Start with the states $$ |+\rangle = |i\rangle + |j\rangle\;\mathrm{ and }\; |-\rangle = |i\rangle - |j\rangle $$ and look at \(\langle + | \mathcal O(t) | +\rangle - \langle - | \mathcal O(t) | -\rangle\).
Even computing \(\rho_{ij}\) is hard! Turns out, sampling is easier: $$ \mathrm{Tr\,} e^{-\beta H} = \sum_{i,j,k,\ldots} \color{green}\left(e^{-\delta H}\right)_{ij} \left(e^{-\delta H}\right)_{jk} \cdots $$
For small \(\delta\), the summand is easily computed. This is a joint distribution over \((i,j,k,\ldots)\). Marginalized, it approximates \(\rho_{ii}\).
(Periodic boundary conditions)
(Open boundary conditions)
One step of time evolution requires \(O(V)\) operations.
With state prep, need to evolve for \(O(T + \Delta^{-2})\) steps.
Characteristically, \(\Delta \sim V^{1/3}\). Per measurement: $$ \color{red} O(V^{5/3}) $$
Without state prep, each quantum computation is now $$ \color{green} O(V T) $$
At the cost of needing to perform many more computations (sampling \(\rho\)).
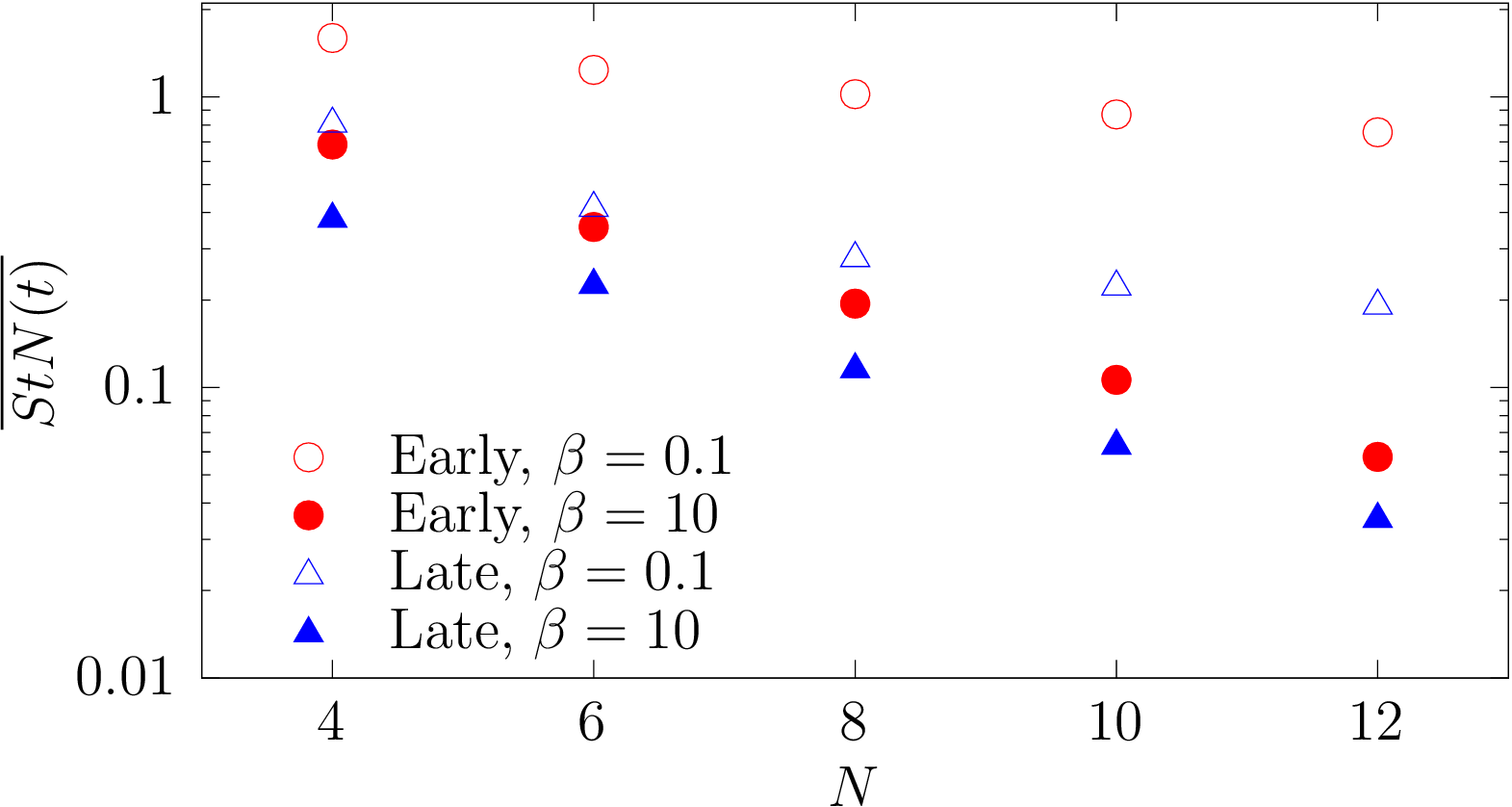
The QC calculation is shorter, but we need many of them.