For a few years now, I’ve had this vague sense that the U.S. flag is at half-staff more often than it used to be. This appears to be true.

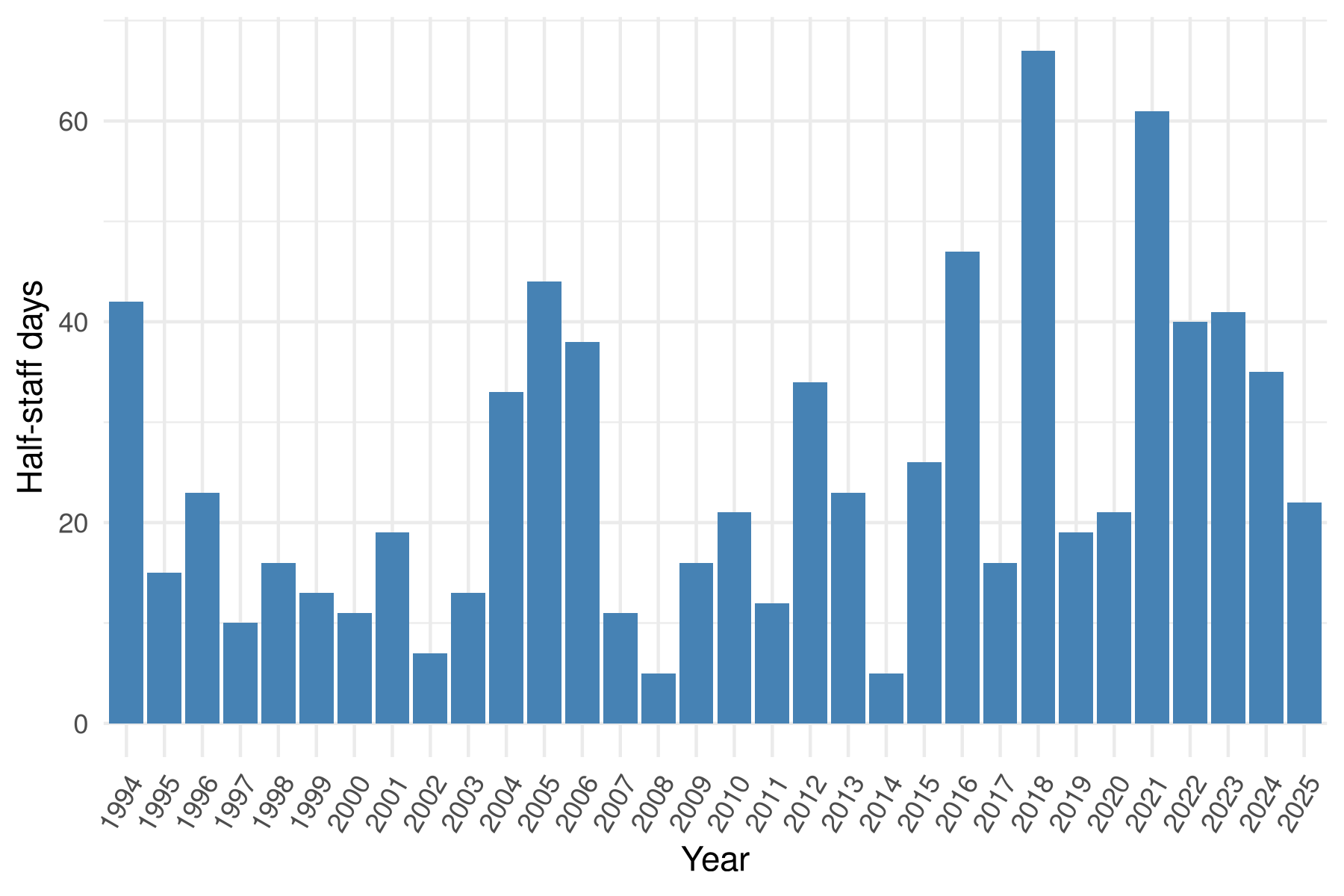
This is generated from presidential proclamations downloaded from the federal register. You can find the CSV I produced by processing this data here. Many of these data points could easily be off by a few days, since much of the processing was automated (by a combination of keyword heuristics to find the relevant proclamations, and then AI to extract dates). Even the stuff that I did by hand can easily be off by a day or two: determining when a particular person was interred, and therefore when the flags were restored to full height, is not always easy! Don’t rely on small differences in the number of days: 20 vs 24 days may not be meaningful.

That being said, there’s a pretty clear overall trend, and two multi-year periods during which the flag was lowered more than 10% of the time: 2004-2006 and 2021-2024. I was born in 1993 and my political memory begins around 2007 (when I began high school). My memory seems to reflect something real: the flag is lowered two or three times more often now, than it was when I was in high school.

I don’t know how seriously to take these trends. On the one hand, a lot of these lowering are due to the deaths of major public figures. In that sense we’re looking at a particular generation that overperformed in public service, and has over the last few years begun to rapidly die off.

On the other hand, it’s hard not to feel that there’s been rising public negativity since 2016. (This has been a favorite topic for Tyler Cowen, for example.) Start-dates vary, but not by that much. Depending the color of your political skin, you associate this negativity either to “woke” or to “Trump”. It is interesting to note that this rising negativity is also reflected in the flag being lowered more often.

Price discrimination accomplishes: redistribution from rich to poor, without government intervention, on a strictly voluntary basis, tending to increase efficiency. What’s not to love?

We already accept price discrimination! Coupons famously serve this purpose (among others), allowing price-sensitive customers to get access to cheaper groceries while still charging the higher price to those who really don’t care. Returns are also a form of price discrimination (if you think about risk as part of the price). And neither of these mechanisms are perfect. Both favor the highly conscientious as much as the price-sensitive, and coupons penalize the desperate and the rushed.

I’m happy to go further. Stores want to discriminate based on price sensitivity, but have trouble doing so, because the really central indicators (income, savings) are not directly visible. So stores have to discriminate based on crude proxies (are you using the app? what part of town are you in?). It’s better than nothing, but we can imagine a better world. Give merchants access to IRS income verification, and let them discriminate based on what they actually care about. Universities do a pretty good job of price discrimination, and this is part of how.

My feelings about price discrimination are not unconditional love. There’s one form of price discrimination which is clearly bad no matter what moral hat I wear. If you charge a higher price based on which customers are unable to shop for alternatives, this is taking advantage of a non-competetive market in a way which doesn’t tend to make the market any more competetive. It’s analogous to the so-called “price gouging” that happens in an emergency, except without the feature of drawing more resources to the task of acquiring necessary goods. This is a pure tax on misfortune.

There’s also the sort of price discrimination made illegal under Robinson-Patman. Recklessly glossing: price discrimination can be unlawful when it has a good chance of suppressing competition. As in the above example, these forms of price discrimination are not increasing efficiency. Fortunately, the example above would incur a great deal of opprobrium in any social climate I can imagine, and price discrimination aiming to suppress competition (as opposed to simply exploiting its absence) is already illegal.

And now for some possible objections. (This isn’t meant to be an exhaustive list; for example, I’m deliberately not replying to “this benefits the corporation at the expense of the consumer”. If you have nothing nice to say…)

Redistribution is bad! This is not obvious. Government redistribution is (presumptively, not always) bad, but this isn’t that. This is a private actor finding that it’s within its own economic interest to perform redistribution. This sort of “third-party redistribution” (distinct from charitable giving!) already happens:

• When people choose to shop at local, or family-run, businesses. (Since the prices are likely a bit higher, there’s also some charitable giving here, but the ordinary surplus that a large chain would have gathered is being redistributed.)
• When stores offer veteran discounts. (In a competetive market, this one is redistribution from the average customer to the veterans, rather than charitable.)
• Insurance. (Insurance is, by definition, redistribution from the lucky to the unlucky.)

Now, it’s plausible that redistribution schemes from rich to poor generally hurt efficiency as a result of the new allocation of resources. But in the case of price discrimination, the act that results in redistribution is itself more efficient. So: assuming we aren’t caring about the welfare benefits of redistribution, it’s still not clear that this form of redistribution is net inefficient.

But it’s unfair! Yes, in a shallow sense. The fact that different people have different amounts of money is also unfair, in an equally shallow sense. If nothing else, there’s a pleasing symmetry here.

What if stores discriminate on the basis of race? Here, in lieu of expressing a strong normative position, I will simply note a polydactyl’s handful of facts.

1. A rational, self-interested actor will generally charge the higher price to the wealthier group.

2. Price discrimination on the basis of race is generally illegal (under the Civil Rights Act of 1964, in a “place of public accomodation”).

3. Laws against racial price discrimination are well-obeyed.

4. Discrimination on the basis of race in higher education is generally illegal (under the same Civil Rights Act of 1964).

5. Laws against discrimination on the basis of race in higher education are not well-obeyed.

6. A rational, self-interested actor will generally favor the wealthier group in college admissions.

I invite you to combine these facts with your moral intuitions and reach whatever conclusion you may. For my part I don’t see a simple moral story into which they all fit, and I don’t believe that price discrimination is substantially related to racial discrimination.

I used to think Schindler’s List a beautiful movie. It’s a story of a man who is, fundamentally, an outlaw. He has little allegiance to the society around him; he is immune to the moral zeitgeist of the time; obeying the law is a matter of practicality, not conscience. He wishes to run a business, but his talent isn’t business, but -schmoozing- networking. He’s nice, in a superficial way, while also not really caring. To be clear, he’s not an outlaw in the “principled rebel” way. He’s a sleaze.

Schindler sees [1] a genuine business opportunity. The Nazis have neglected a valuable workforce. Schindler threads the necessary needles and puts that population to work. They don’t really need to be paid, and Schindler builds a rather profitable business. As he does, he comes to identify with the source of his profit. He realizes the good he has done, and comes to value the good itself more than what led him to it. But we should not forget: what led him to it was a sort of societal sin. He is a criminal. His was a criminal act, not performed for an ideology, but for personal profit.

Schindler saved thousands of lives. Schindler broke the law for personal profit. These are not contradictory parts of a complex man: they are descriptions of the same act. This isn’t a murderer who saves a little girl from an oncoming train, it’s a story of one decision, which is at once a sin and a mitzvah.

That is the essence of the story. It’s beautiful. But rewatching the movie much later, I can’t help but think that I was so focused on the story of Schindler that I missed the substance of the movie. A movie has a story, but also has themes, characterization, and so on. A beautiful story can be told by an ugly movie.

The movie begins, and we meet Oskar. Schindler is calculating, Schindler is greedy. He covets money, he covets gold. He is cunning, certainly, he is also well connected, particularly to other semi-criminal businessmen. He is immune to the demands of his nation, he serves only himself and his bank account. One suspects international connections; at least he is unappreciative of the distinction between a man of one nation (Oskar, a German) and a man of another (Itzhak, a Jew). He is exploitative—the whole movie is about his exploitation! He is manipulative—the whole movie is enabled by his manipulation! He lacks compassion. In short he conforms to a very particular stereotype.

But it’s a movie! Schindler’s character develops. His pleas to his friends to join him don’t appeal to their thirst for money (with which he can no longer fully sympathize): “Come on, I know about the extra food and clothes you give them…”. He views gold as unvaluable: “this is gold! Two more people; they would have given me two for it”. He is self-sacrificing. He even teaches Amon Göth to appreciate that central Christian virtue, forgiveness. “Amon the Good… I pardon you”.

In short, he has adopted Christian values, become a true Christian. It’s a movie, it had to be so. Adopting Christian values is the only path to redemption for someone like him.

[1] Well, in real life, Stern tells him. Let’s not add “business acumen” to the already short list of Schindler’s apparent virtues. But for the consequences of his actions, I’m sure we would consider Schindler a man with no redeeming qualities.