The Kolakoski sequence is a self-descriptive sequence consisting entirely of the digits \(\{1,2\}\). The sequence is organized into “runs”, each consisting entirely of either \(1\)s or \(2\)s, and each of length either \(1\) or \(2\). For example, the beginning of the sequence \[ 1,2,2,1,1,2,1,\ldots \] has five runs, the first of length \(1\) and consisting of \(1\)s, the second of length \(2\) and consisting of \(2\)s, and so on.

The runs always alternate, so that the \(n\)th run consists of \(1\)s if \(n\) is odd, and \(2\)s otherwise. The interesting part of the sequence is in the selection of the lengths of the runs: listing the run lengths recovers the Kolakoski sequence. The run lengths of the sample above are \[ 1,2,2,1,1,\ldots. \] So, to construct the Kolakoski sequence, begin with \(1,2,2\), and then append runs to the end, as described by the bit of the sequence you’ve written down so far. If you like (I certainly do) you can think of this method as having a “read pointer” and a “write pointer”, with the write pointer always appending to the sequence, and the read pointer somewhere in the middle, telling you want to append next. After writing a block, the read pointer advances by one.

The Kolakoski sequence is remarkable for being fantastically difficult to analyze. Define \(N(k)\) to be the number of \(1\)s found in the first \(k\) entries of the sequence. The following question remains open:

What is the asymptotic density of ones in the Kolakoski sequence, defined as \[\lim_{k\rightarrow\infty} \frac{N(k)}{k}\text?\]

It is reasonable to conjecture that the density of ones is \(0.5\). The numerical evidence for this is quite strong. Let’s look at a slightly harder question: assuming that the asymptotic density approaches \(0.5\), how quickly does \(n(k) \equiv N(k)/k\) approach \(0.5\)?

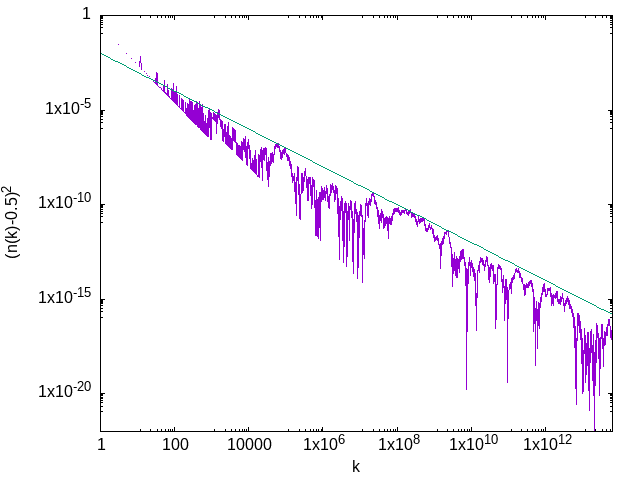
Here we see the deviation of the density from the expected asymptotic value, \((n(k) - 0.5)^2\), plotted on the log-log scale suitable for visualizing power laws. The crude fit (meant to be an approximate upper bound) is to \((100 k)^{-1}\). (With a faster algorithm, the same scaling was a verified for a considerably longer subsequence by Richard Brent.) Note that the sharp lines falling downward are numerical artifacts indicating places where \(n(k) - 0.5\) changes sign.

What should we make of this? Obviously, this is good numerical evidence that the asymptotic density of ones in the Kolakoski sequence is in fact 0.5. It’s suggestive of something more, though. If instead of the Kolakoski sequence, we use a random sequence with each element independently drawn from the uniform distribution on \(\{1,2\}\), we find a very similar picture. In particular, the power-law scaling in which the deviation is typically proportional to \(k^{-1}\) would remain the same, as a consequence of the central limit theorem.

This suggests a picture of the Kolakoski sequence as “essentially random”. Critically, though, the constant in front of the power law would change (to be of order unity). The Kolakoski sequence, then, is consistently much closer to being balanced than we would expect of a random sequence. This is not surprising: the sequence has short-term correlations built in by the requirement that runs alternate, and those correlations forbid long strings of the same digit from occuring, thus forcing the sequence to be more balanced than a random sequence would be.

We can make a more balanced sequence which is nevertheless random by constructing it out of a selected set of subsequences. The naive random sequence is constructed out of all subsequences of length \(1\). If we use subsequences of length \(3\), for example, and exclude the extremely unbalanced \((1,1,1)\) and \((2,2,2)\), then the resulting density of ones \(n(k)\) will again approach \(0.5\) with the CLT-mandated power law, but with a similarly smaller constant out front.

So a slightly more nuanced picture of the statistical behavior of the Kolakoski sequence is that it acts like (in the sense of statistical properties at large \(k\)) a random sequence of many-digit strings, where the permissible strings are selected to be biased towards (but not perfectly) balanced. This is compatible with the fact that any string containing \((1,1,1)\) or \((2,2,2)\) is forbidden by the structure of the alternating runs. Note that more complicated strings are also forbidden, like \((1,2,1,2,1)\), which involves three runs of length \(1\) in a row.

Of course this is extreme extrapolation from a fit extracting a single exponent. Still, as far as I can tell, it’s compatible with what’s known about the sequence.