The choice of opening is supposed to have a lingering effect throughout a game of chess. So much so, in fact, that a game is routinely referred to as “a Sicilian game”, a “Queen’s pawn game”, and so on. Most of the influence of the opening comes from the pawn structure: pawns are relatively immobile, so what structure is created early on is likely stuck for most of the rest of the game.

This is a nice story, but as it is, it’s just a story. How often is the pawn structure destroyed, erasing evidence of the opening? What proportion of games actually have a recognizable opening? How long does the opening linger — is it still visible after 30 moves? In other words: can we quantify this?

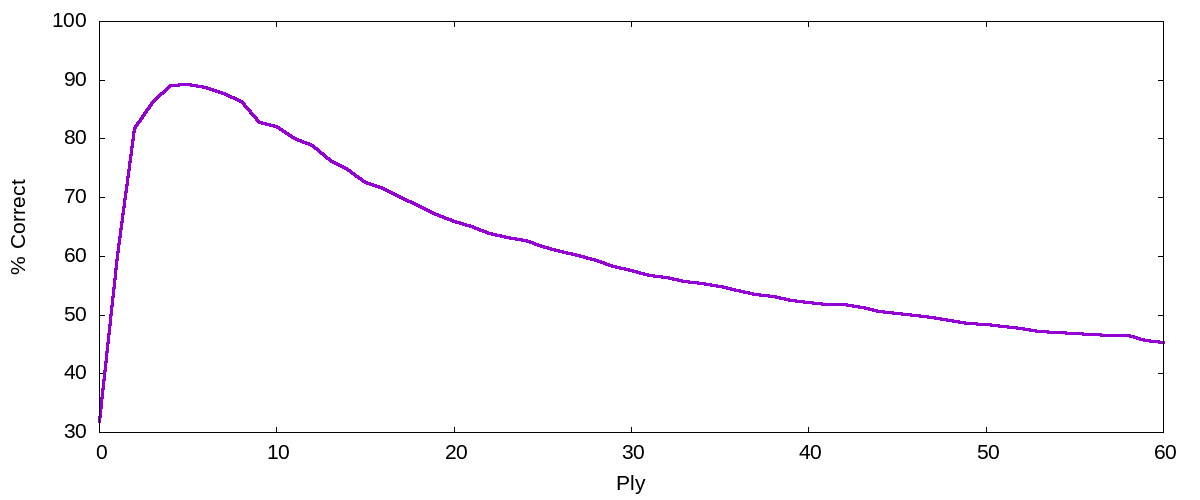
Well, yes. The plot above is a crude measure of how strong the influence of the opening is after some number of moves. (The axis is labelled in “ply” — half-moves — so move 30 is the last shown in the plot.) Obviously there’s no influence before any moves have been played; influence peaks after just a few moves (defining the opening); influence then decays, reaching half its peak strength around move 15.

How is this measure obtained? If you believe that the choice of opening has a large influence on a game even 20 moves later, then you ought to be able to look at a board after 20 moves — without having seen the first part of the game! — and accurately guess the opening. That plot is obtained by teaching a computer to perform that task, and then measuring how well it does. The better it does, the larger the influence of the opening.

A support vector machine is a machine learning algorithm often used for classification. The usual approach is supervised learning. I have a bunch of data points (in this case, chess positions), and I’ve classified them in some way (in this case, according to ECO code). The SVM is trained on this prepared data, and at the end, it can be used to perform the classification task: given a chess position, guess what the opening was.

Now, “guessing what the opening was” isn’t really useful. But whether the SVM works or not… that is interesting information! It’s a crude measure of how easy it is to tell what the opening was, given a position. In other words, it’s a measure of how much influence the opening moves (as opposed to all the other moves) had on the position.

Pawns are supposed to mediate the influence of the opening, so I fed the SVM only information about pawns. (This also makes the training faster, and I’m both lazy and impatient.) Easier than guessing the full ECO code is guessing just the first letter, splitting the openings up into five broad classes, so that’s the categorization the machine was trained on. The plot above shows the percentage of openings correctly classified, as a function of number of moves played to get to the position. This measures, therefore, how easy it is to guess the opening from a position, by looking only at the pawn structure.

My understanding is that the format of the input can have a large impact on the performance of the SVM, so to avoid ambiguity: each position was described as a 64-component vector. Each component corresponds to a single square. A component is \(0\) if there is no pawn on that square, \(1\) if the pawn on that square is white, and \(-1\) if it’s black.

I used libsvm for this experiment, so there’s not really any code to post. I took the data from nikonoel’s database of high-rated Lichess games in June 2020.

Some things to note about this approach.

First of all, guessing the first letter of the ECO code is surely easier than guessing the full code. The absolute success rate will be much lower if the SVM is asked to perform the full classification. My guess is that the shape of the curve also changes, with a much steeper decay before move 10, as opening information that doesn’t affect the pawn structure is quickly lost.

On the flip side, restricting the SVM to looking at pawn structure should weaken its ability to classify openings. This is one reason the graph above peaks at 90%, rather than 100%.

Finally, there’s no guarantee that a different algorithm would have the same success rate. From what I know about the functioning of SVMs, I suspect that this plot comes pretty close to the information-theoretic optimum, but I haven’t actually tested that! Results like these can only be trusted if they’re shown to be robust across many different algorithms; otherwise, we’re looking as much at properties of the SVM as at properties of the game of chess.